Binary Search Tree
Binary search tree is a special kind of tree which is an efficient data structure to organize data for quick search as well as quick updates.
The special property of a Binary search tree is
- Nodes in the left subtree of the root node have a value less than or equal to the root node value.
- Nodes in the right subtree of the root node have a value greater than the root node value.
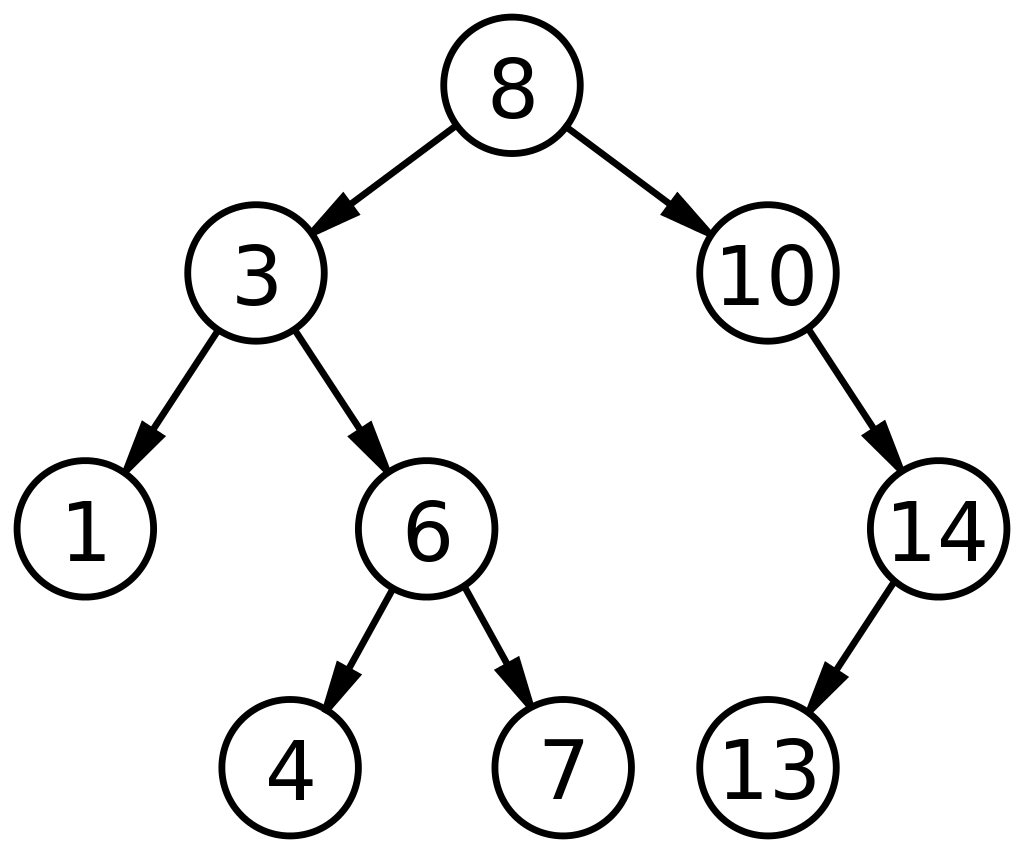
Src : https://commons.wikimedia.org/w/index.php?curid=488330
Why do we Need Binary Search Trees?
Consider a collection of integers which is constantly getting added and deleted , you want to check a particular value from the collection.
Array : 3,5, 2,7
What if we want to check 7 was present in the array.
If we try to apply binary search first we need to sort the array. Sorting an array would take O( N * Log N ) and Binary search in itself will take an additional O(Log N) time for each search operation.
As the array was constantly being added to and deleted from, after update the array looks like below
Array : 3,5, 2,7, 13 , 19 ,38 , 16 ,24 , 46 , 12
Due to new updates the sort operation we performed earlier is outdated. So to apply binary search we need to sort it once again , means O( N * Log N ) cost is added for each update.
So Binary search doesn't work very well for constantly modifying dataset. And Binary tree search is there for the rescue.
If we use a Binary search tree the cost of all the operations will be O(Log N). We will get better performance if the tree is balanced.
Search
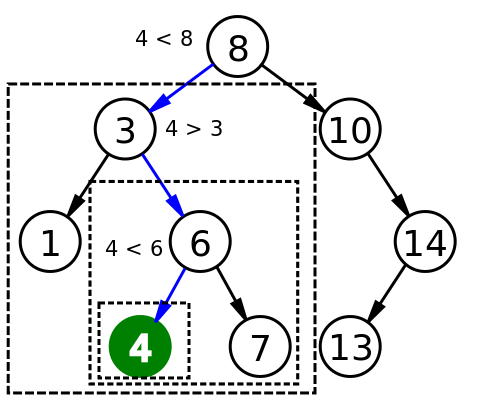
SRC : https://commons.wikimedia.org/wiki/File:Binary_search_tree_search_4.svg
Let's say we want to search 4 from the above BST. We will start traversing from the root node .
Step 1 : Root node value is 8 which is greater than 4 , it means 4 must be present in the left subtree of the current node. So traverse to the immediate left node.
Step 2. Root node value for the current subtree is 3 which is less than 4 , It means 4 must be present in the right subtree of the current node. So traverse to the immediate right node.
Iterate this process until we find 4. So using Balanced BST if there are N nodes at each step we can discard n/2 nodes.
Insertion
New nodes are inserted as leaf nodes in BST . To insert we need to find a suitable position which is very similar to search operation. The only difference in the Insertion operation compared to search is after finding the suitable location we will create a new node.
Deletion
Deleting a node from BST is tricky. Even after deleting a node the property of BST must be conserved.
So consider three cases here
- Node to be deleted has no child node.
- Node to be deleted has one child node.
- Node to be deleted has two child nodes.
Case 1 : Node to be deleted has no child node.
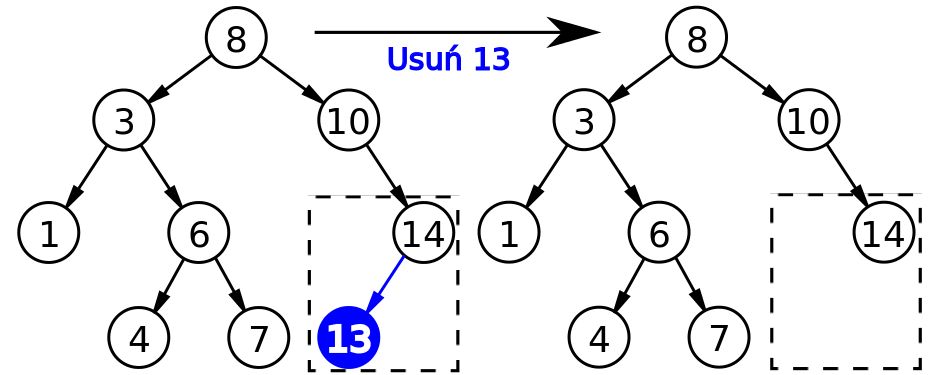
SRC : https://commons.wikimedia.org/wiki/File:Binary_search_tree_delete_13.svg
What if we want to delete 13 which is a leaf node. We need to detach the reference of that node from the parent node and reclaim the memory allocated for node 13.
So deleting a root node is simple.
Case 2 Node to be deleted has one child node.
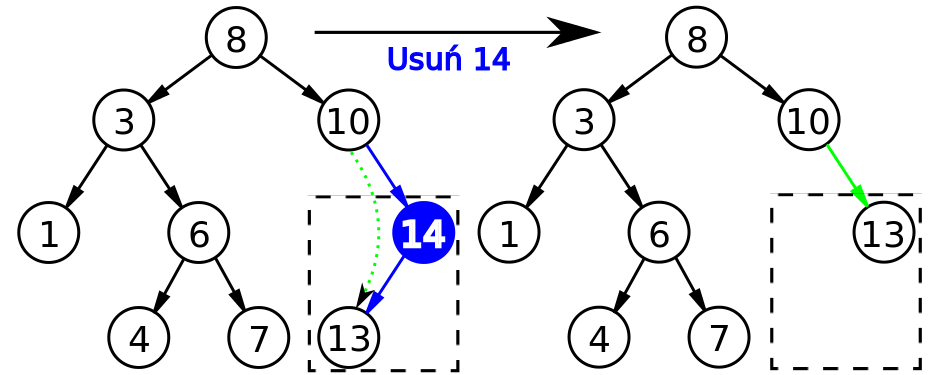
SRC : https://commons.wikimedia.org/wiki/File:Binary_search_tree_delete_14.svg
If the node to be deleted has only one child like 14 in the above case. Link the parent to the child node that is in the above case link node 10 to node 13.
Case 3 : Node to be deleted has two children nodes.
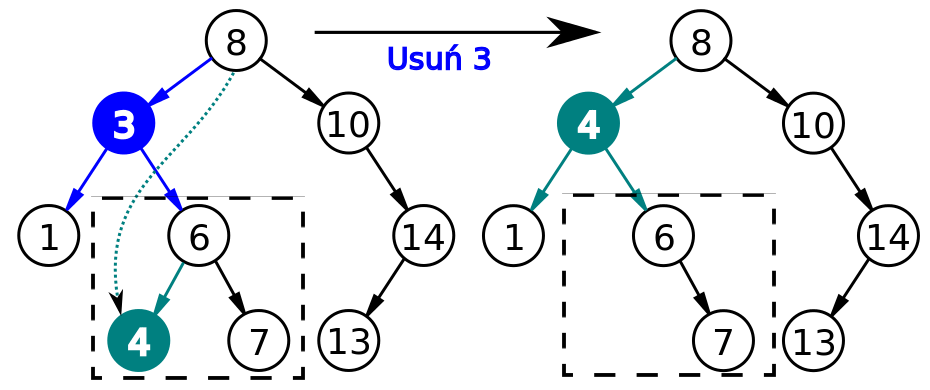
SRC : https://commons.wikimedia.org/wiki/File:Binary_search_tree_delete_3.svg
Visit the right subtree of the deleting node.
Take the minimum value node.
Replace the deleting node with the minimum value node.
In this way take the node with value 4 which is the least valued node and replace it to node 3 as shown in the above image.
Applications of Binary Search Trees
When your data set is dynamic and constantly updated, i.e. there are a lot of insertions and deletions, Binary Search Trees are very useful.
In-order traversal always returns the elements sorted in increasing order.
